1 平面点集的投影

以上讨论了一维点集的情况，下面讨论二维点集\(A = \{ (x_i, y_i) | i=1,2,…N \}\)在任一平面直线 \(l\)上的投影点 \(P=\{ p_i ∈ |i=1,2,…N \} \)的距离方差。

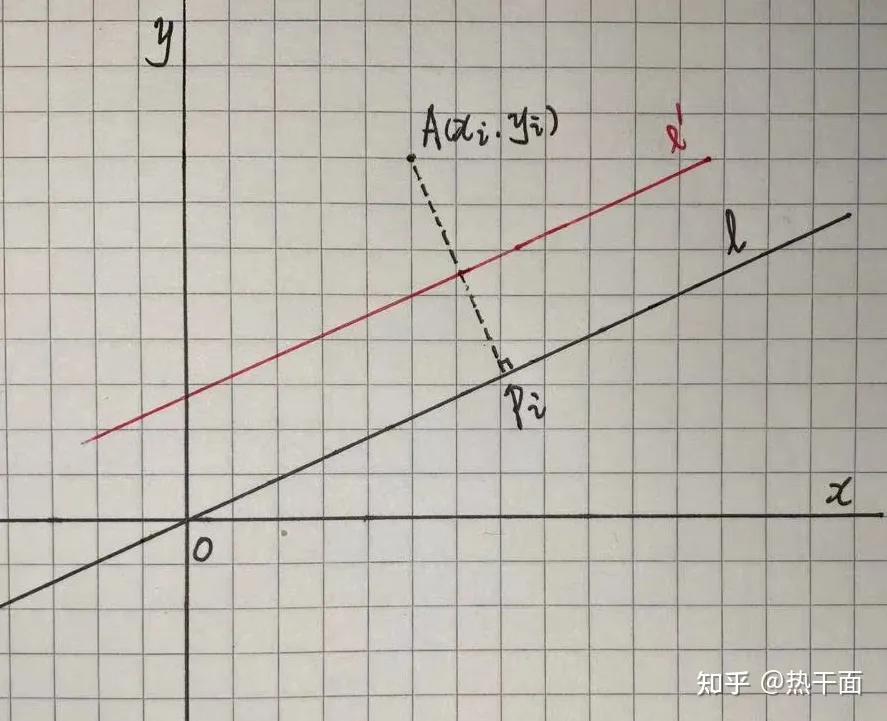
通过前面的讨论可知：分割点必然为投影点\(P=\{ p_i ∈ |i=1,2,…N \} \)的质心；分割线必然垂直于直线\(l\)。根据矢量投影公式可知：

\[ \overrightarrow {O{p_i}} = \frac{{\overrightarrow {O{A_i}} \cdot \overrightarrow l }}{{\left| {\overrightarrow l } \right|}} \]

更进一步求得分割点\(p\)的矢量位置：

\[\overrightarrow {Op} = \frac{1}{N}\sum\limits_{i = 1}^N {\overrightarrow {O{p_i}} = \frac{1}{N}} \frac{{\overrightarrow {O{A_i}} \cdot \overrightarrow l }}{{\left| {\overrightarrow l } \right|}} = \frac{{\overrightarrow l }}{{\left| {\overrightarrow l } \right|}} \cdot \left( {\frac{1}{N}\sum\limits_{i = 1}^N {\overrightarrow {O{A_i}} } } \right)\]

其中 \(\left( {\frac{1}{N}\sum\limits_{i = 1}^N {\overrightarrow {O{A_i}} } } \right)\) 就是二维点集\(A\)的质心。也就是说：分割点是二维点集\(A\)的质心在直线\(l\)上的投影。

考虑更一般的情况：如果存在一条平行于直线\(l^′\) 平行于直线\(l\) ，那么显然二维点集\(A\)在这两条直线上的距离方差不会有任何变化。分割点仍然是质心到直线的投影；分割线的方向仍然垂直于其中任一一条直线。

在这种情况下，不妨将二维点集\(A\)的质心设置为坐标原点，直线\(l\)均通过坐标原点，这样可以简化分析和计算过程。

2 距离方差的极值

三角函数预备知识：

\[\cos 2\alpha = 2{\cos ^2} – 1\]

\[\sin 2\alpha = 2\sin \alpha \cos \alpha \]

\[\sin (\alpha \pm \beta ) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \]

以二维点集\(A = \{ (x_i, y_i) | i=1,2,…N \}\)的质心为原点，设立直角坐标系。直线\(l\)过坐标系原点，其与\(x\)轴的夹角为\(\beta\)。二维点集中任一点\(A_i = (x_i,y_i)\)到原点的距离为\(d_i\)。其在直线\(l\)上的投影点到原点的距离为\(n_i\) 。\(A_i = (x_i,y_i)\)和原点连线与\(x\)轴的夹角为\(n_i\)。显然\(x_i=d_i cos \alpha_i, y_i= d_i sin \alpha_i\)。

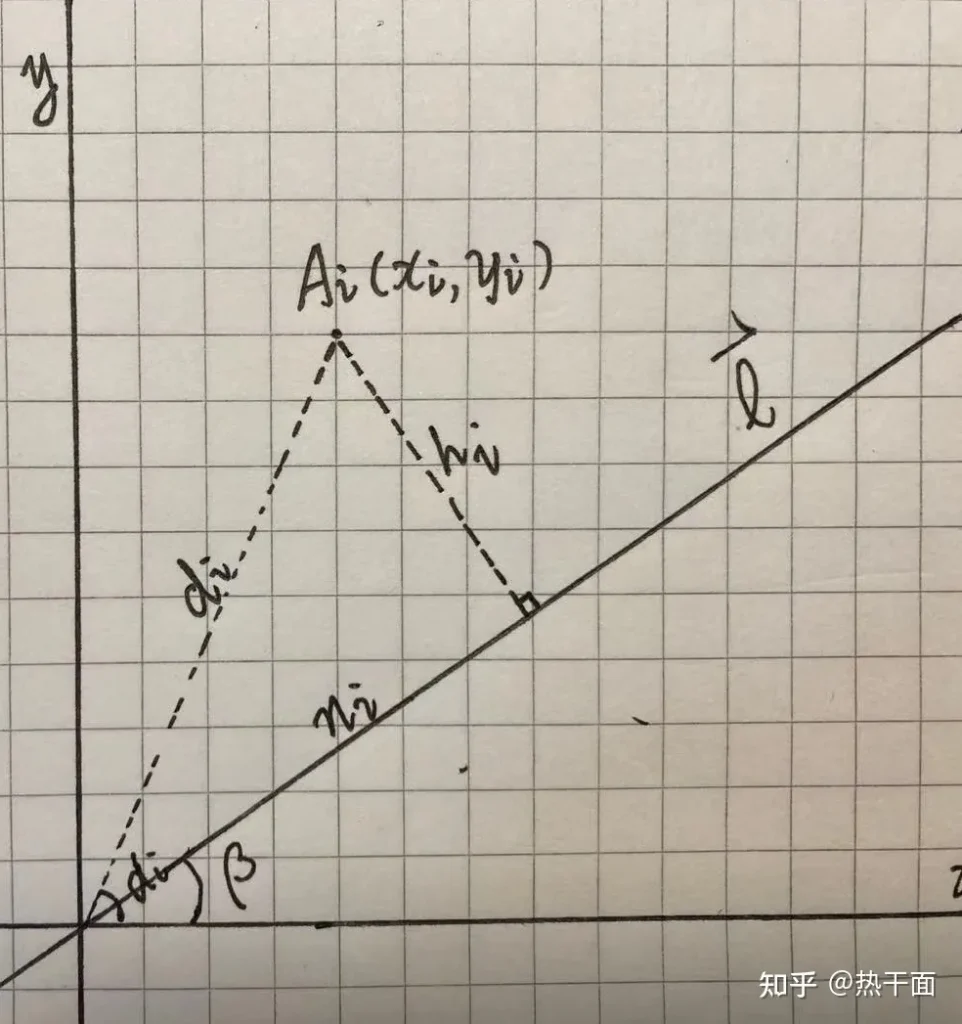
因此有：\(n_i = d_i cos(\alpha_i – \beta)\)。令：

\[H = \sum\limits_{i = 1}^N {n_i^2 } = \sum\limits_{i = 1}^N {d_i^2{{\cos }^2}({\alpha _i} – \beta )} \\ = \sum\limits_{i = 1}^N {d_i^2 \frac {\cos 2 ( \alpha_i – \beta) + 1}{2}} \\ = \frac{1}{2} \sum\limits_{i = 1}^N {d_i^2 [\cos 2 (\alpha_i – \beta) + 1]} \]

现在要求的就是\(H\)的极值。由于\(H\)是关于\(\beta\)的函数，可令\(\frac{d H}{d\beta } = 0\) 。即：

\[\frac{d H}{d\beta }= \frac{1}{2}\sum\limits_{i = 1}^N {d_i^2[ – \sin 2({\alpha _i} – \beta )] \cdot ( – 2)} \\ = \sum\limits_{i = 1}^N {d_i^2\sin 2({\alpha _i} – \beta )} \\ = \sum\limits_{i = 1}^N {d_i^2(\sin 2{\alpha _i}\cos 2\beta – \cos 2{\alpha _i}\sin 2\beta ) = 0}\]

因此可以求得：

\[ tg2\beta = \frac{\sum\limits_{i = 1}^N {d_i^2\sin 2 \alpha_i}} {\sum\limits_{i = 1}^N {d_i^2 \cos 2 \alpha _i} } = \frac {\sum\limits_{i = 1}^N {d_i^2 \cdot 2\sin \alpha_i \cos \alpha_i}} {\sum\limits_{i = 1}^N {d_i^2(\cos ^2 \alpha_i – \sin^2 \alpha_i)} } \\ = \frac{2 \sum \limits_{i=1}^N {(d_i \sin \alpha_i) \cdot (d_i \cos \alpha_i)} }{\sum \limits_{i=1}^N{[(d_i \cos \alpha_i)^2 – (d_i sin \alpha_i)^2 ]}} = \frac{2 \sum \limits_{i=1}^N{x_i y_i}}{\sum \limits_{i=1}^N{(x_i^2 – y_i^2)}}\]

令\(k = \frac{2 \sum \limits_{i=1}^N{x_i y_i}}{\sum \limits_{i=1}^N{(x_i^2 – y_i^2)}}\)，则\(tg 2 \beta=k\)，\(\beta = \frac{1}{2} arctg(k) \)。

当直线\(l\)得夹角\(\beta = \frac{1}{2} arctg(k) \)时，距离方差存在极值。此时是极大值，还是极小值可以利用二阶导数进行判断。

\[ \frac{d^2 H}{d^2 \beta} = \sum \limits_{i=1}^N{d_i^2 cos 2 (\alpha_i – \beta ) \cdot (-2) } \\= -2 \sum \limits_{i=1}^N{d_i^2 ( cos 2 \alpha_i cos 2 \beta + sin 2 \alpha_i sin 2 \beta)} \\ = -2 \sum \limits_{i=1}^N{[d_i^2 (\cos^2 \alpha_i – \sin^2 \alpha_i) \cos 2 \beta + 2 d_i^2 \sin \alpha_i \cos \alpha_i \sin 2 \beta]} \\ = -2 \sum \limits_{i=1}^N{[(x_i^2 – y_i^2) cos 2 \beta + 2 x_i y_i sin 2 \beta]} \\ = -2 [\cos 2 \beta \sum \limits_{i=1}^N{(x_i^2-y_i^2)} + 2 sin 2 \beta \sum \limits_{i=1}^N{x_i y_i}] = – \frac{4}{\sin 2 \beta} \sum \limits_{i=1}^N{x_i y_i} \]

从以上分析可知：必然存在一个距离方差极大值方向和一个距离方差极小值方向，而且这两个方向相互垂直。