作者研究相关系数的最初目标,是想找到一种能够评价”什么样的文字“是词汇的方法。互联网上的文本资料特别丰富,例如:网文小说,各种百科全书等等。但是从网络上检索到的词典就是五花八门,各种词汇混杂在里面。这些词条既不能全信,也不能不信,让人非常纠结。
因此作者想到:程序是否可以通过统计的方法来判定某些文字是常用的词汇?这就需要确定一种基于统计的判定方法。即使这种办法不是完全准确的,也能减轻不少额外的工作量。
有关”相关系数“理论的文章,作者写过两篇:
第一篇文章是在有了灵感之后,经过初步探究后写下的。第一篇里面的错误还是挺多的。在保留原始文章的情况下,作者经过进一步地思考和探究后,写下第二篇文章。读者们可以都参考着看一下。虽然两篇文章有很大的不同,但是基本核心思路是一致的。
一、基本定义
设\( S = \{ {{s_i}|i \in {N^*}} \} \)是指定语料中所有字符串的集合。对于指定的语料,按照一定的统计方式进行统计,得到每个对应字符串的词频集合\( F = \{ {({s_i},{f_i})|i \in {N^*}} \} \),其中\({f_i}\)是字符串\({s_i}\)在语料中出现的频次。该次统计所得的总计数为 \(T\)。具体\(T\) 应如何计算,与具体的统计方法有关,对相关系数的定义并没有影响。
对于字符串子集合\( S^* = \{ {s_1} , {s_2} , …… , {s_N} \} \),定义相关系数\(\gamma \):
\[ \gamma (s|S^*) = \frac{f}{N}\sum\limits_{i = 1}^N {\frac{1}{{{f_i}}}} \]
其中:
- 子符串\(s\)由子字符串集合\( S^* \)按顺序拼接而成。
- \(f\)是字符串\(s\)在语料中出现的频次。且\(f > 0\)。
例如:字符串“我”出现了506822次;字符串“们”出现了194994次;字符串“我们”出现了95808次。那么字符串“我们”的相关系数可以按照如下公式进行计算:
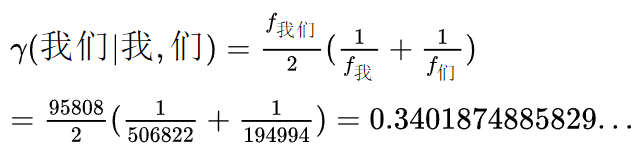
二、拓展定义
由于相关系数的本质是概率,因此可以从字符串对字符串的相关性,拓展至字符串集合对字符串的相关性,乃至字符串集合对字符串集合的相关性。
以字符串集合对字符串为例:
设\( S^* = \{ {{s_i}|i \in {N^*}} \} \)是某个字符串集合。对于指定的语料,按照一定的统计方式进行统计,得到每个对应字符串的词频集合\( F = \{ {({s_i},{f_i})|i \in {N^*}} \} \),其中\({f_i}\)是字符串\({s_i}\)在语料中出现的频次。
现有字符串\(s\),其在语料中的频次为 \(f\) 。那么定义这个集合 \(S^*\)与字符串\(s\)之间的相关系数\(\gamma\):
\[ \gamma ({S^*} \cdot s) = \frac{{\sum\limits_{i = 1}^N {{f_{{s_i} \cdot s}}} }}{2}\left( {\frac{1}{{\sum\limits_{i = 1}^N {{f_{{s_i}}}} }} + \frac{1}{f}} \right) = \frac{{\sum\limits_{i = 1}^N {{f_{{s_i} \cdot s}}} }}{2}\left( {\frac{1}{{\sum\limits_{i = 1}^N {{f_i}} }} + \frac{1}{f}} \right) \]
其中\({f_{{s_i} \cdot s}}\)表明是以集合\(S^*\)中的字符串元素做前缀,与字符串\(s\)拼接后所得字符串在语料中出现的频次。
上述公式中:
(1) 当\( \sum\limits_{i = 1}^N {{f_{{s_i} \cdot s}} = 0} \)时,\( \gamma \left( {{S^*} \cdot s} \right) = 0 \);
此时,相当于只要出现集合\(S^*\)的任一字符串\(s_i\),后面必然不会出现子符串\(s\)。
(2) 当\( \sum\limits_{i = 1}^N {{f_{{s_i}}} = f = } \sum\limits_{i = 1}^N {{f_{{s_i} \cdot s}}} \)时,\( \gamma \left( {{S^*} \cdot s} \right) = 1 \);
此时,相当于只要出现集合\(S^*\)的任一字符串\(s_i\),后面必然会出现子符串\(s\)。
同样按照这个公式可以定义后缀相关系数,以及其他组合相关系数。
三、基本性质
根据相关系数的基础定义,可以知道相关系数\(\gamma\)的一些基本性质。
(1) 相关系数\(\gamma\)与语料的统计方法无关
相关系数公式中并没有出现统计的总计数\(T\)。如果同样的语料按照同样的统计方法再全部统计一遍,不会影响相关系数\(\gamma\)的具体数值。但是不同的语料取向,会在一定程度上影响相关系数\(\gamma\)。
例如:输入大量的公司名称,那么“有限公司”的相关系数会提高很多。而且像“限公”这样无意义的词汇的相关系数也会迅速增加。
(2) 字符串\(s\)所对应的频次\(f \le \{ f_1, f_2,……,f_N \} \)
由于字符串\(s\)由字符串集合\( \{ s_1, s_2,……,s_N \} \)按顺序拼接而得。所以字符串\(s\)所对应的频次不可能超过任何一个字符串集合元素的统计频次。
如果出现了这样的情况,则需要检查统计方法是否出现了问题。
(3) 设\(f_{min} = min(\{ f_i \}) \),\(f_{max} = max (\{ f_i \} )\)。即\(f_{min}\)是字符串集合元素的频次最小值;\(f_{max}\)是字符串集合元素的频次最大值。那么有:
\[ \frac{f}{{{f_{\max }}}} \le \gamma \le \frac{f}{{{f_{\min }}}} \]
这个结论的证明很简单,读者可以自行完成。
(4) 相关系数:\(\gamma \in [0,1]\),即\( 0 \le \gamma \le 1\)。
当且仅当\(f = 0\)时,\(\gamma = 0 \);
另外当且仅当\(f = f_1 = f_2 = …… = f_N\)时,\(\gamma = 1\)。
当\(\gamma = 0 \)时,则称\( \{ s_1, s_2,……,s_N \} \)完全不相关;
当\(\gamma = 1 \)时,则称\( \{ s_1, s_2,……,s_N \} \)完全相关。
注意:这里的“相关”或者“不相关”是基于拼接字符\(s\)而言的。不要与其他数学概念混淆。
(5) 当存在子字符串\(s_j\),其\(f_j = 0\)时,则相关系数\(\gamma\)无意义。
显然,如果拼接字符\(s\)的子字符串\(s_j\)都没有在语料中出现过。那么讨论拼接字符串\(s\)的相关系数\(\gamma\)就显得毫无意义。这个原则,可以归结为“人择原理”。有关“人择原理”,后面还会有详细叙述。
(6) 相关系数\(\gamma\)代表了子字符串的“结合紧密”程度。
相关系数越大,说明子字符串之间的结合程度更高,反之则说明结合程度偏低。利用这个性质,就可以对一个较长的字符串进行“划分”和“组合”,找到相关系数\(\gamma\)的最大值。那么这种“划分”或者“组合”则是最符合统计方法的划分方式。
因此,可以将相关系数用于判断词汇,短语或者句子的划分之上。另外相关系数\(\gamma\)并不排斥“歧义”:虽然各种组合中必然能找到最大值,但对于其他与最大值十分接近的值,也可以用于“划分”。
四、拓展阅读
AlgMain : 相关系数——灵感来源
相关系数的灵感来源,与概率没什么关系,倒是与物理上的电路有一点关系。
AlgMain : 相关系数——数学解释
相关系数\(\gamma\)的定义可以用概率来进行解释。
AlgMain : 相关系数——人择原理
相关系数算法对“人择原理”有很大的依赖性。